円順列とじゅず順列の数を求めます。
問9を少しやさしくした問10を作りました。
以下でこの問題を解きます。
【問10】
(1)玉×2個と●2個と○2個を円形に並べる方法(円順列)は何通りあるか。
(2)更に、それらを連結したじゅずを作る方法(じゅず順列)は何通りあるか。
(1)円順列の数は以下の様にして求めます。
玉×と●と○を並べる席が2+2+2=6箇所あります。
6つの席が固定されている場合に、玉×2つと●2つと残りの玉2つを並べる配置の総数は、
6!/(2!×2!×2!)=6P4/(2!×2!)
=6×5×4×3/(2×2)=90通り
あります。
(第1のタイプ:1回転すると元の配置の形に重なる配置)
玉×と●と○の1つの円順列の配置を1回転すると元の配置の形に重なるが、1/6回転させる毎に、固定した席に対しては、異なる配置になり、1回転するまでに、6つの異なる配置が作られる配置を、第1のタイプの配置とします。
固定席での第1のタイプの配置の数を6で割り算した結果が、第1のタイプの円順列の配置の数です。
(第2のタイプ:1/2回転すると元の配置の形に重なる配置)
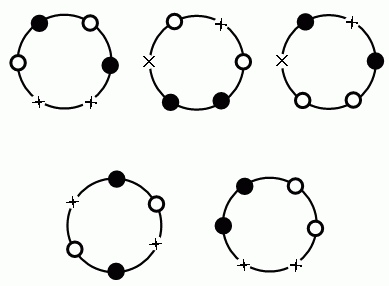
下の2つの円順列の配置では、1/2回転で元の配置の形と同じ形になる。これを第2のタイプの配置とします。
第2のタイプの配置では、1/6回転させる毎に、固定した席に対しては、異なる配置になり、1/2回転するまでに、3つの異なる配置が作られる。
固定席での第2のタイプの配置の数を3で割り算した結果が、第2のタイプの円順列の配置の数です。
第2の タイプの円順列の配置は、上図の2組だけです。
第1のタイプの円順列の数は:
(第1のタイプの円順列の数)
=(固定席での配置の総数-(第2のタイプの円順列の配置の数×3))/6
=(90-(2×3))/6=14
円順列の配置の総数は、この第1のタイプの配置の数に、第2のタイプの円順列の配置の数(2組)を加えた数であり、
14+2=16
組みです。
(2)じゅず順列の数は以下の様にして求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る所定の裏返し線でその円順列の配置を裏返す場合に、
裏返した結果が、裏返す前の円順列の配置に重なるかどうかを調べます。
(第3のタイプ:線対称な形の配置)
下図の6個の円順列の配置は、図に書き加えた点線の裏返し線で裏返した結果が裏返す前の元の配置に重なる線対称な形の配置です。
この第3のタイプの円順列の配置の数は6個のみである。その数が、第3のタイプのじゅず順列の配置の数である。
(第4のタイプ:線対称では無い配置)
円順列の配置のうち、第3のタイプの配置以外の配置を第4のタイプの配置とする。
第4のタイプの配置では、円順列では、元の配置と、裏返した後の配置とは異なるので、2倍の数の配置として数えられている。
すなわち、第4のタイプの配置では、円順列の配置の数が、じゅず順列の配置の数の2倍あり、
第4のタイプの配置のじゅず順列の配置の数は、円順列の配置の数を2で割り算した数である。
第4のタイプのじゅず順列の配置の数は:
((円順列の配置の総数)ー(第3のタイプの円順列の配置の数))/2
=(16-6)/2=5
あります。
一方、第3のタイプの円順列の配置の数=じゅず順列の配置の数=6個でした。
全部のじゅず順列の数は、
(じゅず順列の総数)=
=(第4のタイプのじゅず順列の配置の数)+(第3のタイプのじゅず順列の配置の数)
=5+6=11
場合の数と確率
リンク:高校数学の目次
問9を少しやさしくした問10を作りました。
以下でこの問題を解きます。
【問10】
(1)玉×2個と●2個と○2個を円形に並べる方法(円順列)は何通りあるか。
(2)更に、それらを連結したじゅずを作る方法(じゅず順列)は何通りあるか。
(1)円順列の数は以下の様にして求めます。
玉×と●と○を並べる席が2+2+2=6箇所あります。
6つの席が固定されている場合に、玉×2つと●2つと残りの玉2つを並べる配置の総数は、
6!/(2!×2!×2!)=6P4/(2!×2!)
=6×5×4×3/(2×2)=90通り
あります。
(第1のタイプ:1回転すると元の配置の形に重なる配置)
玉×と●と○の1つの円順列の配置を1回転すると元の配置の形に重なるが、1/6回転させる毎に、固定した席に対しては、異なる配置になり、1回転するまでに、6つの異なる配置が作られる配置を、第1のタイプの配置とします。
固定席での第1のタイプの配置の数を6で割り算した結果が、第1のタイプの円順列の配置の数です。
(第2のタイプ:1/2回転すると元の配置の形に重なる配置)
下の2つの円順列の配置では、1/2回転で元の配置の形と同じ形になる。これを第2のタイプの配置とします。
第2のタイプの配置では、1/6回転させる毎に、固定した席に対しては、異なる配置になり、1/2回転するまでに、3つの異なる配置が作られる。
固定席での第2のタイプの配置の数を3で割り算した結果が、第2のタイプの円順列の配置の数です。
第2の タイプの円順列の配置は、上図の2組だけです。
第1のタイプの円順列の数は:
(第1のタイプの円順列の数)
=(固定席での配置の総数-(第2のタイプの円順列の配置の数×3))/6
=(90-(2×3))/6=14
円順列の配置の総数は、この第1のタイプの配置の数に、第2のタイプの円順列の配置の数(2組)を加えた数であり、
14+2=16
組みです。
(2)じゅず順列の数は以下の様にして求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る所定の裏返し線でその円順列の配置を裏返す場合に、
裏返した結果が、裏返す前の円順列の配置に重なるかどうかを調べます。
(第3のタイプ:線対称な形の配置)
下図の6個の円順列の配置は、図に書き加えた点線の裏返し線で裏返した結果が裏返す前の元の配置に重なる線対称な形の配置です。
この第3のタイプの円順列の配置の数は6個のみである。その数が、第3のタイプのじゅず順列の配置の数である。
(第4のタイプ:線対称では無い配置)
円順列の配置のうち、第3のタイプの配置以外の配置を第4のタイプの配置とする。
第4のタイプの配置では、円順列では、元の配置と、裏返した後の配置とは異なるので、2倍の数の配置として数えられている。
すなわち、第4のタイプの配置では、円順列の配置の数が、じゅず順列の配置の数の2倍あり、
第4のタイプの配置のじゅず順列の配置の数は、円順列の配置の数を2で割り算した数である。
第4のタイプのじゅず順列の配置の数は:
((円順列の配置の総数)ー(第3のタイプの円順列の配置の数))/2
=(16-6)/2=5
あります。
一方、第3のタイプの円順列の配置の数=じゅず順列の配置の数=6個でした。
全部のじゅず順列の数は、
(じゅず順列の総数)=
=(第4のタイプのじゅず順列の配置の数)+(第3のタイプのじゅず順列の配置の数)
=5+6=11
場合の数と確率
リンク:高校数学の目次





0 件のコメント:
コメントを投稿